Un problema colorido
domingo, 12 de mayo de 2013
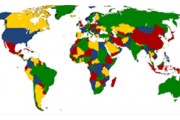
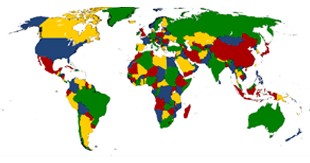
Como cualquiera que garabateó una fila tras otra de los cálculos sabe, los problemas matemáticos pueden requerir mucho tiempo para ser resueltos. Si crees que esto es malo, piensa por un momento en Kenneth Appel y Wolfgang Haken. Su problema era tan largo que sólo un ordenador podía calcularo, y la prueba no se puede verificar manualmente por un matemático humano. El gran problema consistía en cómo colorear un mapa con tan solo cuatro colores - también conocido como el teorema de los cuatro colores.
¿Cuatro es suficiente?
Todo comenzó en 1852, cuando un matemático y botánico llamado Francis Guthrie coloreó en un mapa de los condados de Gran Bretaña. Guthrie intentaba evitar el uso del mismo color en las comarcas adyacentes, y se dio cuenta que necesitaba un mínimo de cuatro colores para hacerlo. Guthrie se preguntó si era posible dibujar un mapa en el que se necesitaran más de cuatro colores para evitar las regiones vecinas de idéntico color. Le pidió a su hermano Federico, también matemático, y el problema se extendió al debate de la comunidad matemática en general. Nadie tenía una respuesta.
El enigma quedó sin resolverse hasta 1879, cuando un matemático Inglés llamado Alfred Kempe publicó una prueba en la revista American Journal of Mathematics. Por desgracia, la prueba sólo duró hasta 1890, cuando Percy Heawood descubrió un fallo en la lógica. Con el trabajo de Kempe, Heawood fue capaz de demostrar que se necesitan no más de cinco colores, pero el teorema de cuatro colores se mantuvo sin demostrar.
Dibujo un espacio en blanco
¿Por qué era este un trabajo para los ordenadores, y no de los lápices de colores? Es fácil demostrar que tres colores o menos no son suficientes para llenar un mapa - echar un vistazo a este sencillo ejemplo:
El intento de dibujar un mapa de cinco colores con rapidez conduce a problemas, sin embargo. No importa cuanto lo intente, todos los mapas parecen ser totalmente coloreado por sólo cuatro tonos. Pero, ¿cómo sabemos que no hay un mapa muy complicado por ahí, un contraejemplo al acecho en el cuadro de la coloración? La demostración del Teorema de los cuatro colores significa mostrar que tal contraejemplo no puede existir, y para ello necesitamos una manera de describir matemáticamente mapas.
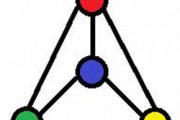
Generalmente utilizamos el mundo "graph" para describir los diagramas como un bar o un gráfico circular, sino un gráfico matemático es un conjunto de puntos unidos por líneas. Estos puntos y líneas se llaman vértices y aristas, y resulta que podemos convertir cualquier mapa de un gráfico por dibujar las regiones como vértices y los límites como los bordes. Por ejemplo, aquí está el mapa que se muestra arriba dibujado en un gráfico:
Volviendo mapas en gráficos significa que no tenemos que preocuparnos por su forma actual, y puede concentrarse en la relación entre las regiones. Matemáticos de principios de los 20 th siglo utilizaron las técnicas de la teoría de grafos para mostrar que cualquier mapa con menos de un cierto número de regiones sería sólo necesitar cuatro colores - pero que aún quedan un número infinito de mapas para ver!
Encontrar un atajo
Lo matemáticos necesitaban era una forma de reducir este número infinito a algo más manejable. En 1976 en la Universidad de Illinois, Kenneth Appel y Wolfgang Haken fueron capaces de demostrar que cualquier mapa puede ser reducido a un conjunto de 1.482 tipos básicos. Se dieron cuenta de estos bloques de construcción se podrían utilizar para hacer cualquier mapa imaginable, por lo que si todo 1482 sólo necesitaba cuatro colores, también lo hacía cada mapa.
Sólo había un problema. Comprobación de estas 1.482 mapas sería una tarea increíblemente largo, incluso para un ejército de matemáticos en completarse. En cambio, Appel y Haken programar una computadora para hacer la coloración. El análisis se llevó 1.200 horas de tiempo en la computadora, pero después de una larga espera llegó el resultado: todos los 1482 mapas necesarios sólo cuatro colores. Simple pregunta de Francis Guthrie había sido contestada, un siglo después de que él propuso por primera vez.
No era una pregunta que necesita una respuesta particular - después de todo, los cartógrafos felizmente habían coloreando por año - pero el teorema de los cuatro colores es importante para un par de razones. El trabajo en los gráficos ayudó a definir un área de las matemáticas llamado topología , que se utiliza para estudiar todo, desde la forma del universo para el movimiento de los robots. Más significativamente, el Four Teorema Color marcó el primer uso importante de una computadora en una prueba matemática. Muchos matemáticos estaban descontentos que sólo otro equipo podría examinar la plena prueba de errores. ¿Y si hubiera un error en el software, o una pieza defectuosa de hardware? Exhaustivamente que atraviesa todas las combinaciones posibles tampoco parece "correcta" para algunos matemáticos, ya que le dio la respuesta correcta, pero no una verdadera comprensión del problema. Computadoras, ya se han utilizado para probar muchos otros teoremas, pero su uso plantea interrogantes sobre lo que realmente significa "hacer" matemáticas.
Fuente: Mathscareers
Enlace relacionado: Kenneth Appel, el matemático que coloreaba mapas