¿Matemáticas para aprender a defraudar o a detectar fraudes?
miércoles, 20 de marzo de 2013
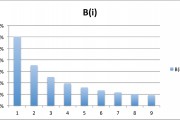
Cambiar demasiados números en documentos financieros puede resultar arriesgado si uno no conoce ciertas matemáticas. Muy a menudo, los números que aparecen en este tipo de documentos siguen cierta regla matemática, llamada ley de Benford o ley del primer dígito significativo. Si uno se olvida de seguir la regla, entonces los números no pasarán ciertos tests estadísticos y es probable que sean examinados con detenimiento por un hipotético agente fiscal. La ley de Benford, también conocida como ley del primer dígito, asegura que en muchos (pero no todos) tipos de números que proceden de cantidades medibles observadas en la naturaleza o producidas por las actividades desarrolladas por los seres humanos, los números que empiezan por 1 aparecen de forma mucho más frecuente que los que comienzan por 2, que a su vez son más frecuentes que los que empiezan por 3. Y que la frecuencia para cada cifra inicial va disminuyendo hasta ser mínima para el 9.
Esta regularidad estadística es sorprendente, incluso para los expertos, por ir contra la intuición humana. Esta regla se observa en muchos conjuntos de números, como las potencias de 2 o los números de Fibonacci.
¿Por qué?
A día de hoy se tienen explicaciones satisfactorias para este hecho y en el pdf adjunto las compartimos con el lector.
En cuanto a todo lo escrito en estos últimos tiempos sobre la Ley de Benford en relación a la presunta contabilidad fraudulenta del Partido Popular, merece la pena leer el artículo publicado por Abel Fernández en el blog Sistenia: "La Ley de Benford y la presunta contabilidad B del PP"